Teorema. 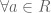
, berlaku
 Bukti.
Bukti.
Menurut sifat identitas penjumlahan berlaku
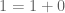
. Akibatnya,

.
Jadi,
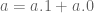
[sifat distributif]
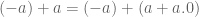
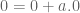
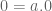 Teorema.
Teorema. Bilangan 0 tidak memiliki invers perkalian
Bukti.
Dari teorema di atas berlaku

untuk setiap a. padahal bila 0 mempunyai invers berarti
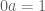
untuk suatu a, akibatnya

. Hal ini tidak mungkin terjadi dalam bilangan real, sehingga haruslah pernyataan 0 tidak mempunyai invers merupakan pernyataan yang benar.
Teorema. Jika

dan
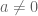
, maka
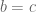 Bukti.
Bukti.
Diketahui

dan
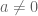
, artinya a mempunyai invers. Sehingga dapat dituliskan,
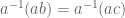

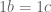
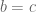 Teorema.
Teorema. 
dan

, berlaku
 Bukti.
Bukti.
Kita tunjukkan bahwa

adalah negative dari

, artinya

Menurut hukum distributif,

Jadi,
 Teorema.
Teorema. 
dan

, berlaku
 Bukti.
Bukti.
Kita buktikan bahwa
![[(-a) + (-b)] + (a + b) = 0 [(-a) + (-b)] + (a + b) = 0](http://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+0&bg=ffffff&fg=555555&s=0)
seperti berikut,
![[(-a) + (-b)] + (a + b) = [(-a) + (-b)] + (a + b) [(-a) + (-b)] + (a + b) = [(-a) + (-b)] + (a + b)](http://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = (-a) + (-b) + b + a [(-a) + (-b)] + (a + b) = (-a) + (-b) + b + a](http://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%28-a%29+%2B+%28-b%29+%2B+b+%2B+a&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = (-a) + 0 + a [(-a) + (-b)] + (a + b) = (-a) + 0 + a](http://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%28-a%29+%2B+0+%2B+a&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = (-a) + a [(-a) + (-b)] + (a + b) = (-a) + a](http://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%28-a%29+%2B+a&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = 0 [(-a) + (-b)] + (a + b) = 0](http://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+0&bg=ffffff&fg=555555&s=0) Teorema.
Teorema. 
jika dan hanya jika
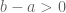 Bukti.
Bukti.
Jika

, maka menurut sifat pada bilangan berlaku

. oleh karena itu didapatkan
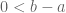
. yang tidak lain yaitu
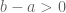
. Sebaliknya, jika
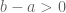
, maka
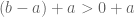
. dan diperoleh
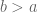 Teorema.
Teorema. 
dan

, maka
 Bukti.
Bukti.
Jika

, maka
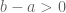
. Akibatnya, menurut sifat pada bilangan didapatkan

. sama dengan

. Sehingga

. Jadi menurut teorema sebelumnya, diperoleh
 Teorema.
Teorema. Jika
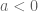
, maka
 Bukti.
Bukti.
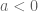
maka
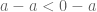
. diperoleh
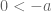
. Sama dengan
 Teorema.
Teorema. Jika
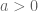
, maka
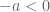 Bukti.
Bukti.
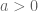
maka

. diperoleh
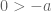
. Sama dengan
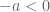 Teorema.
Teorema. 
dan
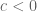
, maka
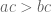 Bukti.
Bukti.
Jika

, maka
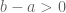
. Padahal
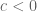
. Maka

. maka
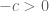
. Akibatnya didapatkan
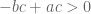
. Jadi menurut teorema sebelumnya, diperoleh
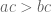


Tidak ada komentar:
Posting Komentar