Matematika: Bukti Theorema Phytagoras

Teorema Pythagoras berbunyi pada suatu segitiga siku-siku berlaku sisi miring kuadrat sama dengan jumlah kuadrat sisi-sisi lainnya. Secara umum, jika segitiga ABC siku-siku di C maka teorema Pythagoras dapat dinyatakan $AB^2 = AC^2 + BC^2$ .
Teorema Pythagoras ini adalah teorema yang sangat terkenal. Teorema ini akan sering digunakan dalam menghitung luas bangun datar. Selain digunakan dalam perhitungan pada bangun datar, perhitungan pada dimensi 3 atau yang lain juga sering menggunakan teorema Pythagoras. Banyak buku-buku menuliskan teorema ini sebagai $c^2 = a^2 + b^2$ . Dengan c adalah sisi miring.
Bukti dari teorema ini sangat bermacam-macam. Sangat banyak cara untuk membuktikan teorema Pythagoras ini. Di sini akan diberikan beberapa bukti teorema Pythagoras. Dari bukti yang sangat mendasar sampai bukti yang cukup rumit. Kebanyakan bukti teorema Pythagoras adalah pengembangan dari bukti-bukti inti (bukti-bukti dasar).

Bukti 1

Disediakan 4 buah segitiga siku-siku. Perhatikan gambar di atas. 4 segitiga di atas adalah segitiga yang sama. Mempunyai sisi-sisi a, b dan c. dan sisi c merupakan sisi miring dari segitiga tersebut. Ketiga segitiga disampingnya adalah hasil rotasi 90, 180 dan 270 derajat dari segitiga pertama.
Luas masing-masing segitiga yaitu $\frac{ab}{2}$ . Sehingga luas 4 segitiga tersebut adalah $2ab$ .
Segitiga-segitiga tersebut kita atur sedemikian sehingga membentung persegi dengan sisi c seperti gambar berikut.

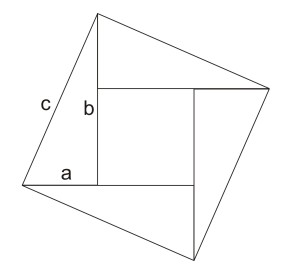
Perhatikan gambar hasil susunan 4 segitiga tersebut. gambar tersebut membentuk sebuah persegi dengan sisi c. dan didalamnya ada persegi kecil. Panjang sisi persegi kecil tersebut adalah $(b-a)$ .
Secara langsung kita dapat menentukan luas persegi besar tersebut, yaitu $c^2$ . Dan secara tidak langsung, luas persegi besar dengan sisi c tersebut adalah sama dengan luas 4 segitiga ditambah luas persegi kecil yang mempunyai sisi $(b-a)$ . Sehingga diperoleh,

$c^2 = 2ab + (b-a)^2$
$c^2 = 2ab + b^2-2ab + a^2$
$c^2 = b^2 + a^2$

Bukti 2

Perhatikan gambar. Gambar tersebut adalah gambar 2 persegi. Persegi yang besar adalah sebuah persegi yang mempunyai panjang sisi a, dan persegi kecil mempunyai panjang sisi yaitu b.
Luas persegi yang besar tentunya adalah $a^2$ . Dan luas persegi kecil adalah $b^2$ . Sehingga luas bangun diatas adalah $b^2 + a^2$

Kedua persegi tersebut kita gabungkan. Dan kita buat garis sedemikian sehingga seperti pada gambar. Sisi c menjadi sisi miring dari segitiga tersebut. kemudian kita potong segitiga-segitiga tersebut. dan kita pindahkan ke bagian atas dan samping kanan seperti pada gambar berikut.

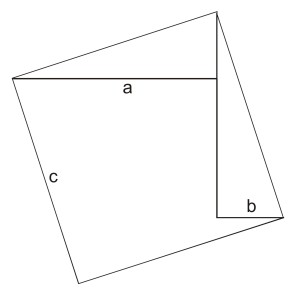
Luas persegi dengan sisi c tersebut tentunya adalah $c^2$ . Karena 2 persegi pada awal tadi adalah sama dengan 1 persegi besar dengan sisi c diatas, maka tentunya luas 2 persegi pertama sama dengan luas persegi besar dengan sisi c tersebut.
sehingga, $c^2 = b^2 + a^2$


Bukti 3

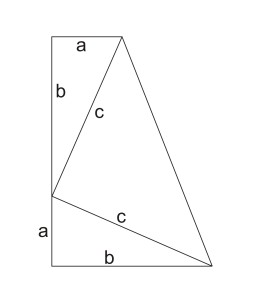
Gambar tersebut adalah gambar sebuah trapesium yang dibentuk dari 3 segitiga. Luas trapesium tersebut adalah $\frac{1}{2}(a+b)(a+b)$ . dicari menggunakan rumus luas trapesium. Yaitu setengah dikalikan dengan jumlah sisi yang sejajar dikali tinggi trapesium. Mencari luas bangun datar diatas dapat juga menggunakan jumlah luas segitiga (perhatikan gambar). yaitu

$\frac{1}{2}ab+ \frac{1}{2}ab+ \frac{1}{2}c^2$ .

Luas yang dihitung adalah tetap. Yaitu bentuk trapezium tersebut. sehingga haruslah kedua luas yang dicari dengan langkah yang berbeda itu harus sama. Diperoleh,

$\frac{1}{2}(a + b)(a + b) = \frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}c^2$
$\frac{1}{2} (a^2+ 2ab + b^2) = ab + \frac{1}{2}c^2$
$\frac{1}{2}a^2+ ab + \frac{1}{2}b^2 = ab + \frac{1}{2}c^2$
$a^2 + b^2 = c^2$

Laman

Kamis, 01 Maret 2012

Bukti Theorema Phytagoras

Tidak ada komentar:

Posting Komentar