Akar dari suatu persamaan dapat dicari dengan menggunakan beberapa cara. Dengan pemfaktoran atau rumus 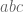 . Atau juga bisa menggunakan rumus melengkapkan kuadrat sempurna. Tetapi untuk jumlah akar-akar atau hasil kali akar-akar dapat dicari menggunakan rumus.
. Atau juga bisa menggunakan rumus melengkapkan kuadrat sempurna. Tetapi untuk jumlah akar-akar atau hasil kali akar-akar dapat dicari menggunakan rumus.
Jika  dan
dan  merupakan akar-akar dari persamaan
merupakan akar-akar dari persamaan 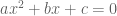 , maka
, maka
Jika  dan
dan  merupakan akar-akar dari persamaan
merupakan akar-akar dari persamaan 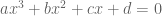 , maka
, maka
Jika  dan
dan  merupakan akar-akar dari persamaan
merupakan akar-akar dari persamaan 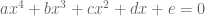 , maka
, maka
Jika 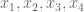 dan
dan  merupakan penyelesaian atau akar-akar dari persamaan
merupakan penyelesaian atau akar-akar dari persamaan 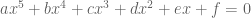 , maka
, maka
dan seterusnya.
Tentunya kalian pasti bisa meneruskan kelanjutan rumusnya. Rumus ini membentuk suatu pola untuk polinom pangkat yang bertambah besar.


Tidak ada komentar:
Posting Komentar